What are time and space complexities ?

What is Big O notation?

In 2020, I started putting my focus on data structures and algorithms and this is gonna be my very first data structure-related blog.

If you have taken some algorithms-related courses, you may probably hear of the word *Big O notation*. Well even if you have never heard, I hope after reading this you can probably get a basic idea of what it is.

Introduction

Big O notation is used to determine how fast an algorithm or your piece of code is. Remember speaking of how great and efficient your code is, the usage of Big O notation can vary in different cases.

Efficiency can determine by various factors like

• CPU usage of our programs
• Memory usage of our programs
• Network usage of our programs
• Disk usage of our programs

If you are a database developer, you may define efficiency in terms of how much memory your program uses. If you are a web developer building a performant website your terms of efficiency may be how much network traffic your program uses or how long your end-user has to wait for your website to load.

Big O is to determine how the runtime scales to the input size of our functions.

Imagine you have to transfer a 100GB load of some important business data from one of your offices to another office. The transfer time may vary based on how big your data size is.

If you are living in a great place with a better internet connection, your transfer rate may be really fast and if your internet connection is terrible then you will be waiting for hours to transfer your data. So how do we determine how fast your programs are without considering any of the external factors?

Let's say in the above example, instead of transferring your data through the internet, you are going to transfer it physically by sending a delivery man with a USB to the other office.

In this case, the transfer time will be constant and no matter if it is 10GB or 100GB, the transfer time will be the same as long as your USB stick is enough to hold the data. There is no external interference.

Transferring data over the internet can take longer and longer depending on the size of the data but the catch here is the delivery man may be slow or fast in this case, transferring data always takes the same amount of time no matter how slow or how fast the guy is. But the time requires by the internet scales linearly as the data size or the input size grows.

So big O is to determine the complexity of your code in algebraic terms especially when the input size tends toward a particular value or infinity.

Describing your code in algebraic terms.

To understand what Big O notation let's take a look at some of the examples in the code. Throughout the whole blog, I am gonna be using Javascript to demonstrate some of the examples but you don't really
have to worry about what language you are gonna be using while talking about Big O.

Take a look at a function where it adds all the numbers in the array.

function addNumbers(arr) {
    var sum = 0;
    for (var i = 0; i < arr.length; i++) {
        sum += arr[i];
    }
    return sum;
}

In the above example, there is a function to add up all the numbers in an array. The runtime of this function is O(n) because it has to iterate through the array once to add up all the numbers.

The longer the array is, the more executions there will be.

Check out the example below where we add the numbers in two arrays.

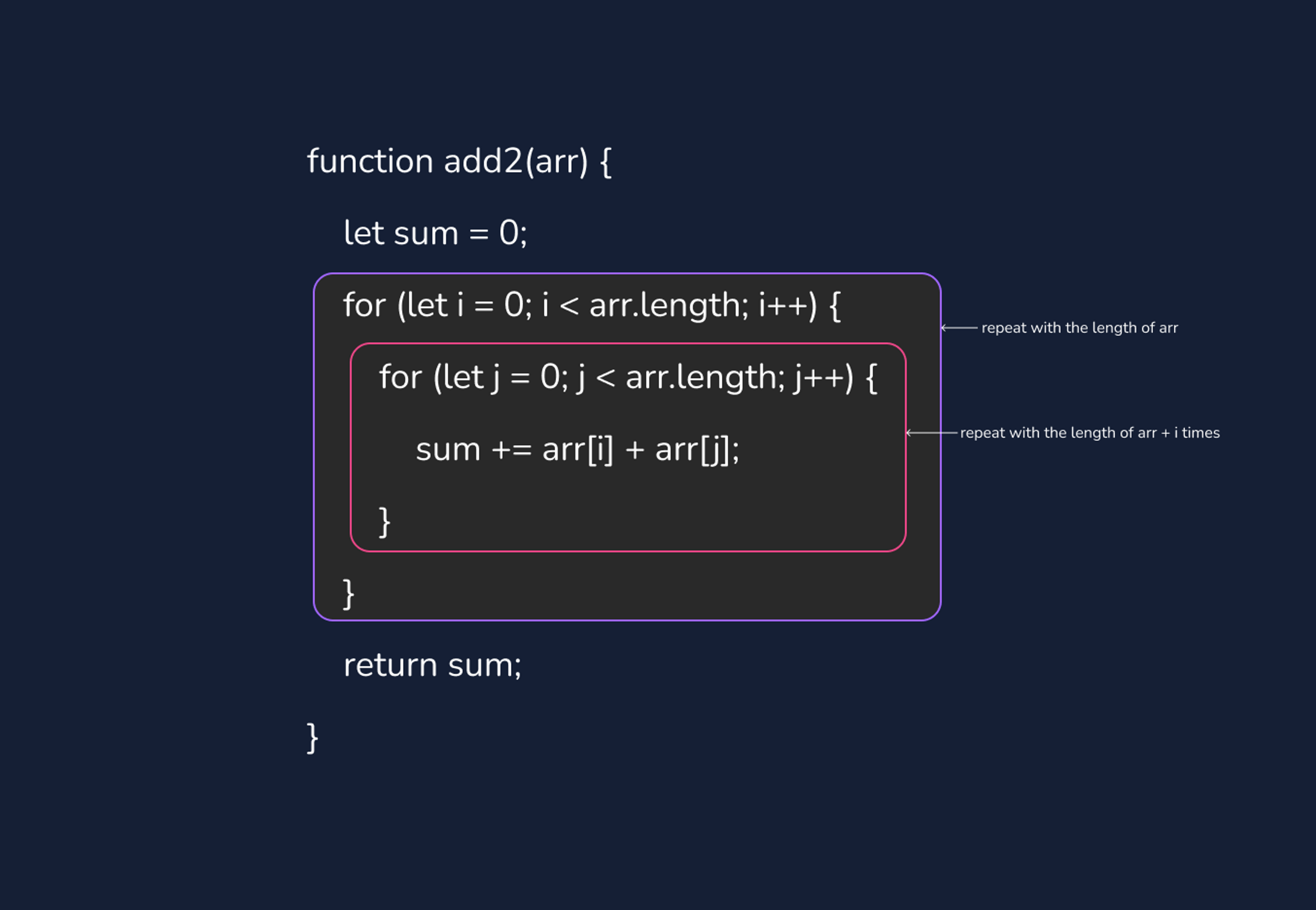
function add2(arr) {
    let sum = 0;
    for (let i = 0; i < arr.length; i++) {
        for (let j = 0; j < arr.length; j++) {
            sum += arr[i] + arr[j];
        }
    }
    return sum;
}

In the above example, we can say the runtime of this function is O(n²) because it has to iterate through the array twice.

How do we determine n?

So let's take a deeper look at how you can determine the running time or complexities of a piece of code.

function add(num1, num2) {
  let total = num1 + num2;
  return total;
};

If each statement is "simple" (only involves only basic operations ) then we can say the time for the statement is constant.

In programming, there are a lot of operations that are constants. For example,

1. math operations
2. accessing an array via index
3. accessing an object via a key
4. pushing and popping an array
   

So in the above code, we can breakdown into

1. look for num 1
2. look for num 2
3. add num 1 and num 2
4. return the total

Now that we have identified our code let's look at the Big O for each of the statements. The complexity for each of the statements is O(1) because they are all just simple operations that only happen once.No matter how big the num1 and num2 they only run once. We can say

O(1 + 1 + 1 + 1) = O(4) = O(1)

So how did we get from O(4) to O(1)? While talking about big O we always assume the worst-case scenario. O(4) is O(4 * 1).

In big O way, we can

1. Assume the worst
2. Remove constants
3. Use different terms for inputs
4. Drop any nondominant

Let's take a look at other complexities

What is the big O of 2n² + 3n?

In the about expression, 3n is a constant representing three instances of O(n). And 2n² is a constant representing two instances of O(n²). So we can drop the constant and we get

O(2n² + 3n) = O(n²)

Best case and worst case

Some functions may require a different amount of time on different calls. Look at the code below.

function find(arr, num) {
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] === num) {
      return true;
    }
  }
  return false;
}

For example, if you are finding a number in an array, sometimes (worst case) you may have to loop through all the elements in the array if
the element you are looking for is at the end of the array. Otherwise (best case) if it's at the start of the array the complexity of that call will be a lot better.
In general, we may want to consider all the best-case, average-case, and also worst-case time requirements.

When do constants matter?

Big O is to determine how fast your code is. Recalling that when we use Big O we don't care about constants and low-order terms. Because the problem size is sufficiently large enough for us to not consider them.

However, what if two pieces of code have the same Big O even though one of them is always faster than the other? For example, one algorithm has the expression of O(n) and the other has O(4n + 1). For both of the
algorithms, the time complexity is O(n). The first one is a lot faster than the second one. In this case, while deciding which one is faster, we will have to take into account the constants and low-order terms.

When two algorithms have different time complexities, the constant and low-order terms are important only when the problem size is small.

Common Big O functions

Constant time O(1)

As we discussed earlier the algorithms or operations are considered to be the instantaneous or constant time when they are not dependent on the size of the input data and the time required to run is the same every single time.

Linear time O(n)

If the number of operations increases linearly with the input size, for example, 100 operations for a list that is 100 items long, then it is linear complexity.

Quadratic time O(n²)

If operations have to perform a linear time operation for each value in input, not just for the input itself. We can generally say that's O(n²).

Logarithmic time O(log n)

Imagine finding a word in a dictionary. We find the word by picking a random point about halfway through. Then we look at the left half whether we passed the first alphabet or not. If we didn't then we look at the right half and if we did we check the left half, and by dividing and conquering we proceed until we find the word.

function binarySearch(arr, num) {
    let start = 0;
    let end = arr.length - 1;
    let mid = Math.floor((start + end) / 2);
    while (arr[mid] !== num && start <= end) {
        if (num < arr[mid]) {
            end = mid - 1;
        } else {
            start = mid + 1;
        }
        mid = Math.floor((start + end) / 2);
    }
    return arr[mid] === num;
}

I am gonna try to blog more about search algorithms later on the blog as much as I can so that's for the binary search.
O(log(N)) is that the time goes up linearly when n grows up exponentially.

Space Complexity and Big O

So far we talked about time complexity and how to determine the time complexity of a piece of code. Let's talk about space. While time complexity talks to the time required to run a piece of code or how to run time scales with the input size. Space complexity is the space required to complete the algorithm or operations.

function add(num1,num2){
    return num1 + num2;
}

With the same psychology can say that the space complexity of the algorithm is O(1). Because our variables are evaluated only once and the space required by the code does not depend on the input size.

function find2(arr, num) {
    let obj = {};
    for (let i = 0; i < arr.length; i++) {
        obj[arr[i]] = true;
    }
    return obj[num] === true;
}

The space complexity for the about code gonna be O(n).Because we are creating an object with key-value pairs depending on the input array.

When time and when space?

Of course, depending on the usage and requirement of our algorithm, sometimes we might choose space complexity over time complexity. Sometimes your algorithm may need to perform a specific task fast in a certain amount of time, we may want the time complexity of the algorithm to be better.
If you are coding for IoT hardware with low memory, you may want to optimize the algorithm for space complexity.

Related Articles