Implementing Heaps : A Comprehensive Guide
Jul 16, 2023Arkar
CS
Learn how to create a min heap and their operations
On this page
In this article, let's talk about heaps and what they do. Heaps are a way to keep things organized based on how important they are. For example, in an emergency room, patients are usually sorted based on the severity of their conditions. To help with this, a heap can be used to organize patients according to their priority level. The most critical patients are placed at the top of the heap, and whenever new patients come in, they are added to the heap and sorted based on their condition's severity.
In task management programs, heaps help organize tasks by importance, so that the most important ones get done first. Heaps have many uses in sorting algorithms, operating systems, and compilers. In compilers, during program execution, it uses heaps for memory allocations. Using heaps allows the compiler to manage memory better while running the program.
Consider the example below with the tasks array. If we used a list instead of a heap to keep track of the tasks, we would have to search through the list every time we wanted to find the task with the highest priority because lists do not have a built-in way to keep the highest priority item at the top. We would have to go through the entire list to find the task with the highest priority and remove it.
Using a heap to manage tasks guarantees that the top task always has the highest priority. This makes it easy to access it without searching through the entire heap. Additionally, when the top task is removed from the heap, the next highest priority task is automatically moved to the top.
const tasks = [
{ name: "task1", priority: 2 },
{ name: "task2", priority: 3 },
{ name: "task3", priority: 1 },
{ name: "task4", priority: 4 },
{ name: "task5", priority: 2 }
];Creating a heap
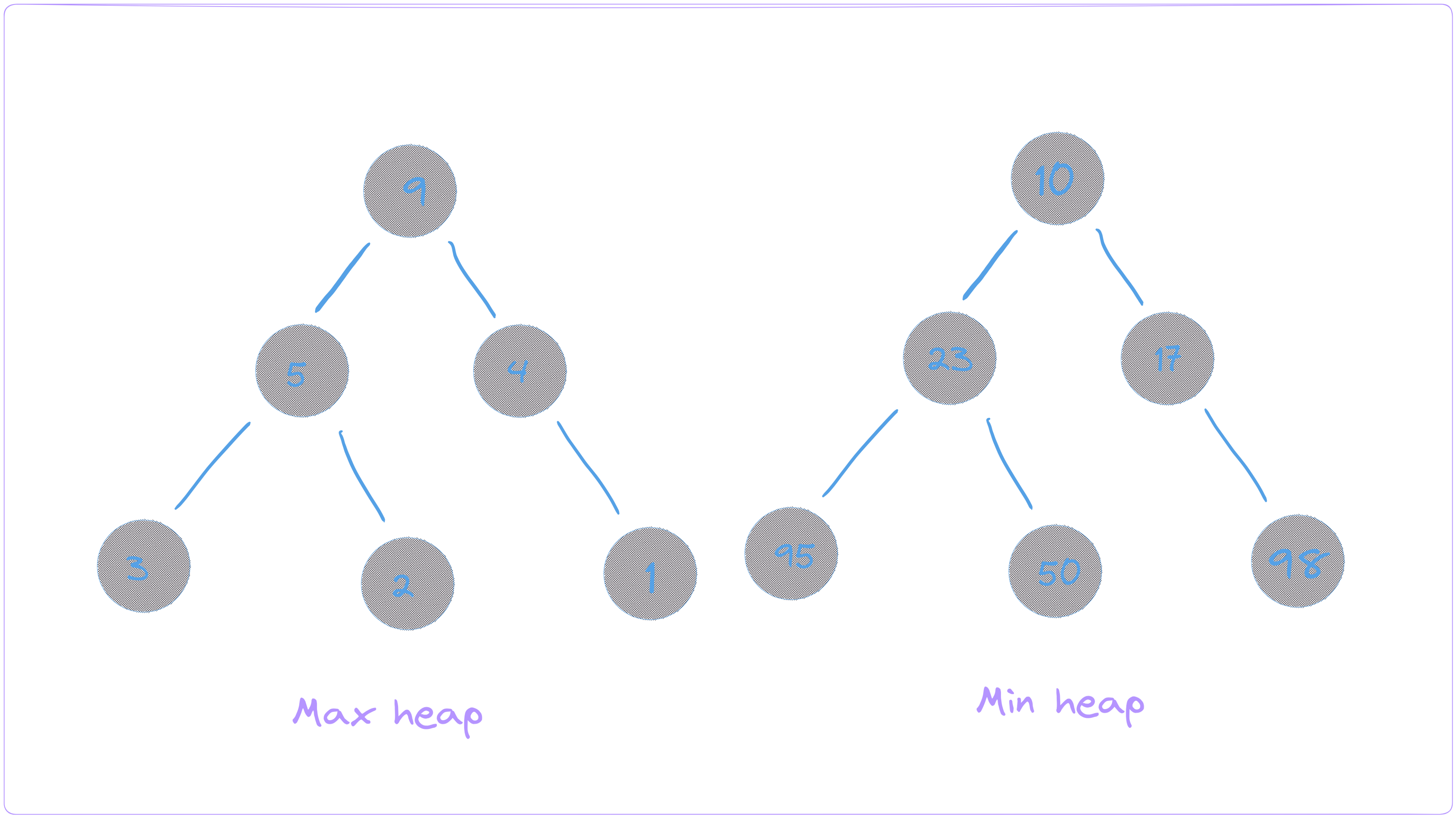
The heap data structure is a way to organize data in a tree-like manner. There are two types of heaps: min heap and max heap. In a min heap, the smallest value is at the top, while in a max heap, the largest value is at the top. One important thing to note about heaps is that, unlike binary trees, they only need to maintain a consistent ordering. A heap does not require that the left child be smaller than the right child or that the left and right subtrees be balanced. As long as every parent node is smaller than its children in a min heap or larger than its children in a max heap, the heap is considered valid.
In this article, I will create a min heap and guide you through the process to help you get a better understanding of heaps.
Heaps are commonly illustrated as trees, but their implementation often uses arrays for efficiency. One thing I love most about implementing heaps using arrays is how it changes my understanding of trees. Instead of thinking about trees in terms of nodes and pointers, we can now think of a tree as a logical structure represented by an array.
Let’s take a look at how we can represent elements in an array as nodes.
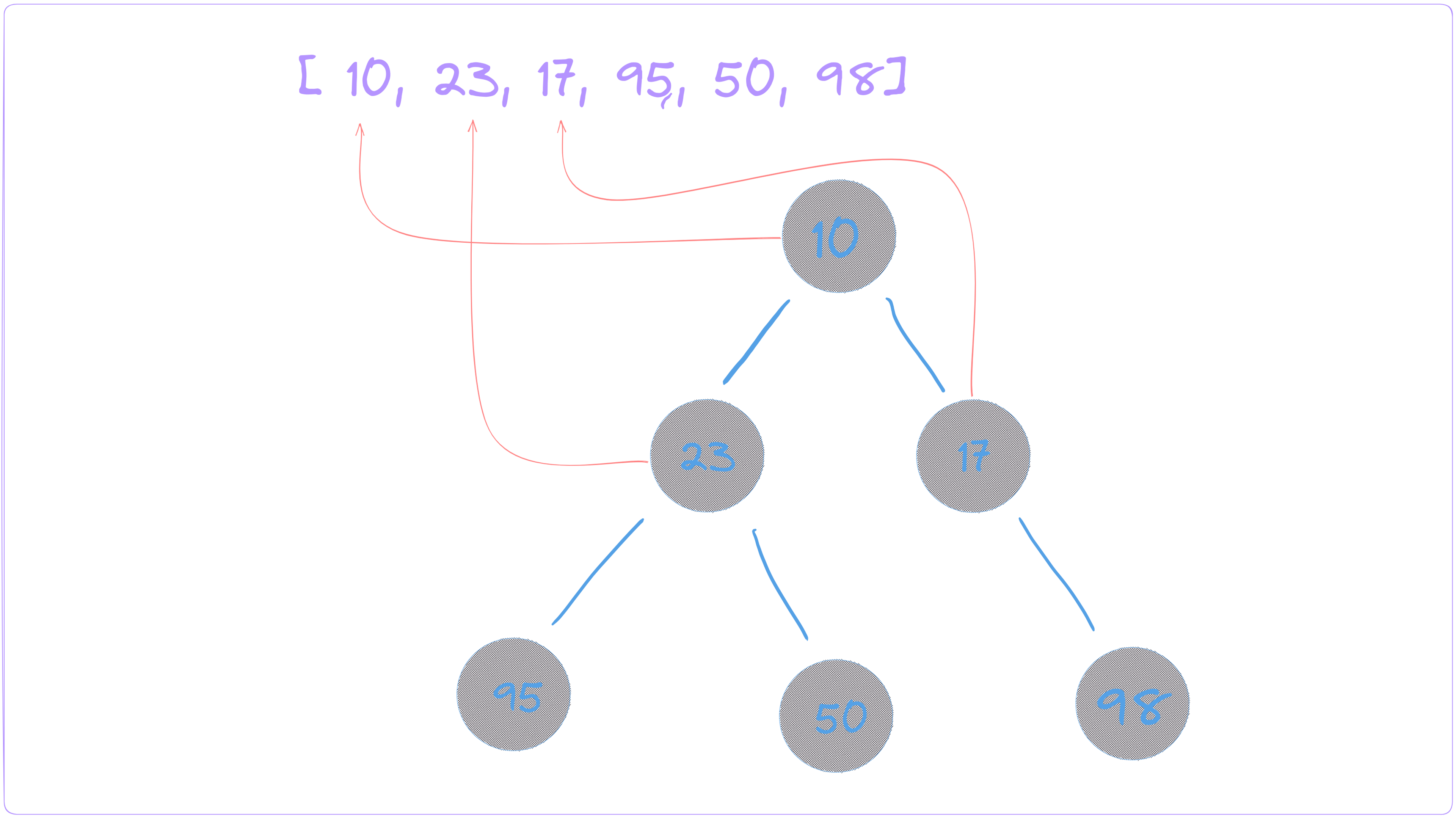
Heaps are commonly illustrated as trees, but their implementation often uses arrays for efficiency. One thing I love most about implementing heaps using arrays is how it changes my understanding of trees. Instead of thinking about trees in terms of nodes and pointers, we can now think of a tree as a logical structure represented by an array.
Let’s take a look at how we can represent elements in an array as nodes.
[10,23,70,95,50,98]The root of the heap is 10, which is at index 0. Its left child is 23, which is at index 2*0+1=1, and its right child is 70, which is at index 2*0+2=2. The left child of 23 is 95, which is at index 2*1+1=3, and the right child of 23 is 50, which is at index 2*1+2=4. The left child of 70 is 98, which is at index 2*2+1=5, and the right child of 70 is not present as it would be at index 2*2+2=6 which is out of the array's bounds.
For this demo, I will be using Typescript for implementation.
export class MinHeap {
public length: number;
private data: number[];
constructor() {
this.data = [];
this.length = 0;
}
private leftChild(index: number): number {
return index * 2 + 1;
}
private rightChild(index: number): number {
return index * 2 + 2;
}
private parent(index: number): number {
return Math.floor((index - 1) / 2);
}
}Adding an element to a heap
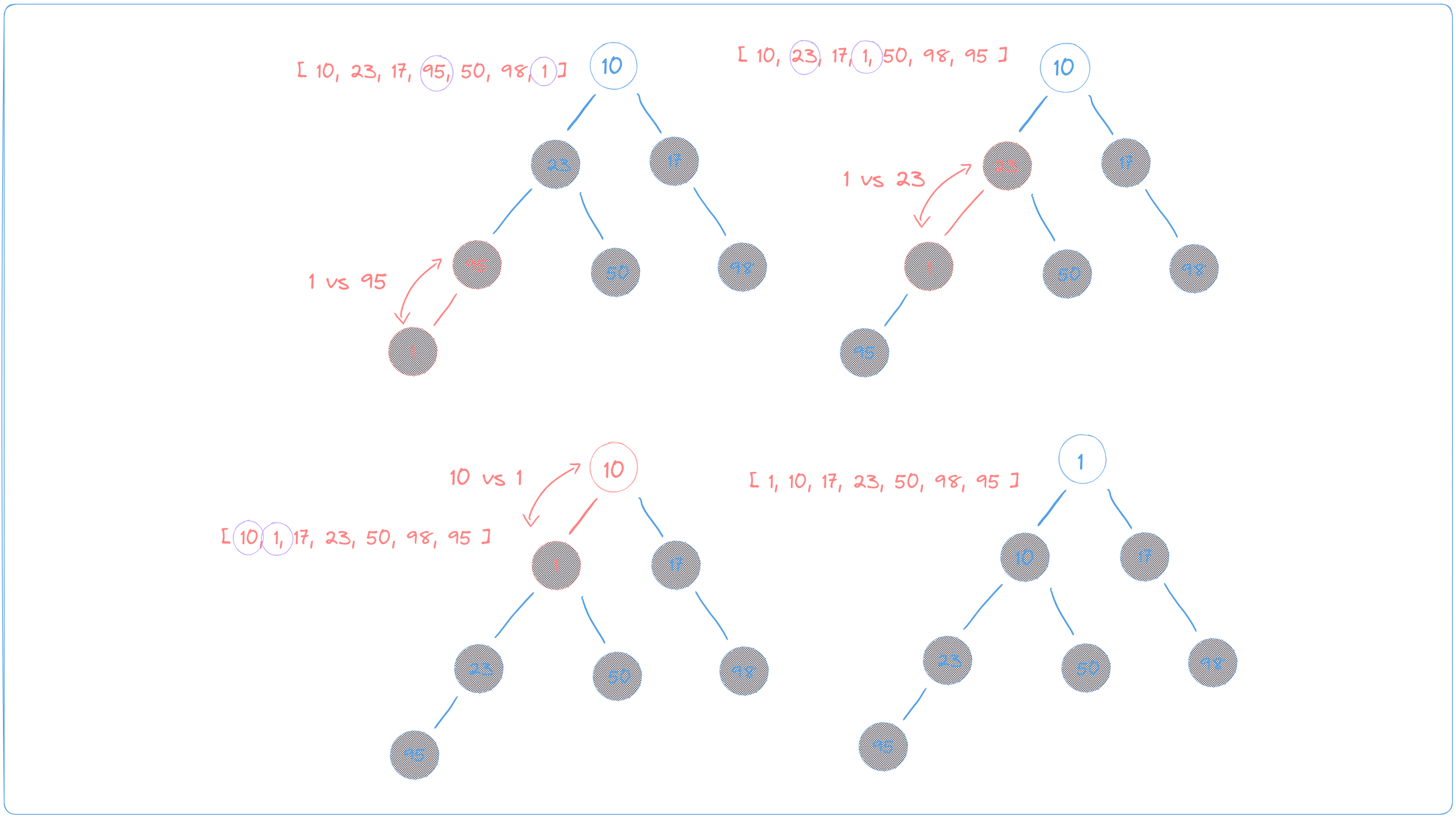
To add an element to a heap, we can add it to the end of the array representation of the heap and then "bubble up" the element to its correct position. In the example below, we add the number 1 to the heap. We start at the bottom and gradually move up, making sure that the value is in the correct position according to the heap's requirements. If necessary, we swap positions along the way.
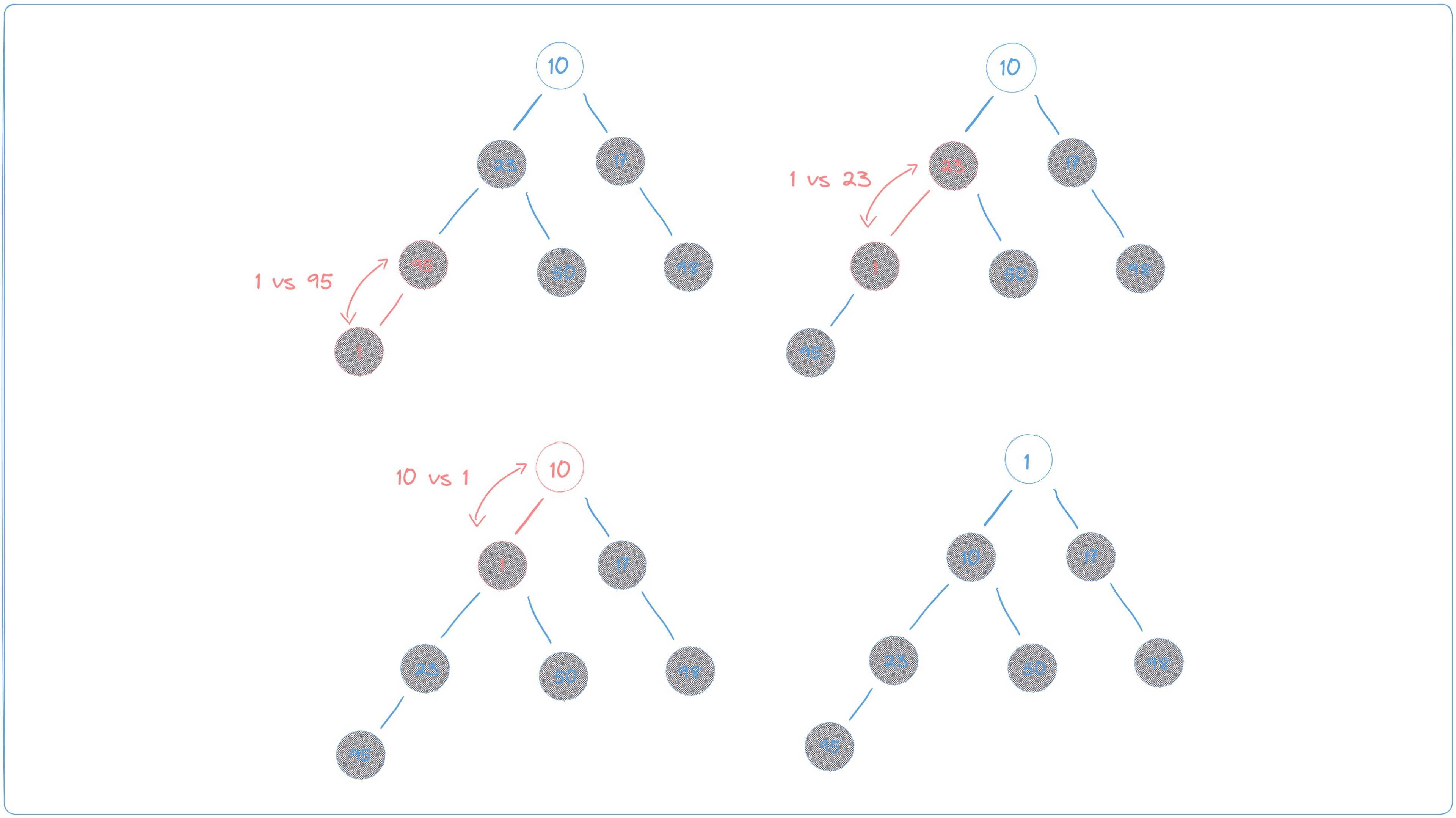
Using an array-based implementation of heaps offers greater efficiency in terms of both time and space complexity than a tree-based implementation. This is because arrays are contiguous blocks of memory, which means that accessing elements in an array is faster than traversing nodes in a tree.
private heapifyUp(idx: number): void {
if (idx === 0) {
return;
}
const p = this.parent(idx);
let pValue = this.data[p];
const v = this.data[idx];
if (pValue > v) {
this.data[idx] = pValue;
this.data[p] = v;
this.heapifyUp(p);
}
}Here is how the code for inserting an element into a heap.
export class MinHeap {
public length: number;
private data: number[];
constructor() {
this.data = [];
this.length = 0;
}
insert(value: number): void {
this.data[this.length] = value;
this.heapifyUp(this.length++);
}
private heapifyUp(idx: number): void {
if (idx === 0) {
return;
}
const p = this.parent(idx);
let pValue = this.data[p];
const v = this.data[idx];
if (pValue > v) {
this.data[idx] = pValue;
this.data[p] = v;
this.heapifyUp(p);
}
}
private leftChild(index: number): number {
return index * 2 + 1;
}
private rightChild(index: number): number {
return index * 2 + 2;
}
private parent(index: number): number {
return Math.floor((index - 1) / 2);
}
}Removing an element from the heap
To remove the top element from the min heap, we can check its value against its children and swap positions if necessary, as explained earlier. This process can also be done recursively, starting with the left and right children, and swapping positions as needed until the element is in the correct position. Below is the code for heapifyDown() that performs this recursive operation:
private heapifyDown(idx: number): void {
let lIdx = this.leftChild(idx);
let rIdx = this.rightChild(idx);
if (idx >= this.length || lIdx >= this.length || rIdx >= this.length) {
return;
}
let lValue = this.data[lIdx];
let rValue = this.data[rIdx];
let v = this.data[idx];
if (lValue < rValue && v > lValue) {
this.data[idx] = lValue;
this.data[lIdx] = v;
this.heapifyDown(lIdx);
} else if (rValue < lValue && v > rValue) {
this.data[idx] = rValue;
this.data[rIdx] = v;
this.heapifyDown(rIdx);
}
}To use heapifyDown(), we follow these steps:
- Find the indices of the left and right children of the current element.
- Compare the values at these indices to find the smallest child.
- If the value of the smallest child is less than the value of the current element:
- Swap their positions.
- Recursively call
heapifyDown()on the smallest child's index.
- Keep doing this until the element is in its correct position or has no children.
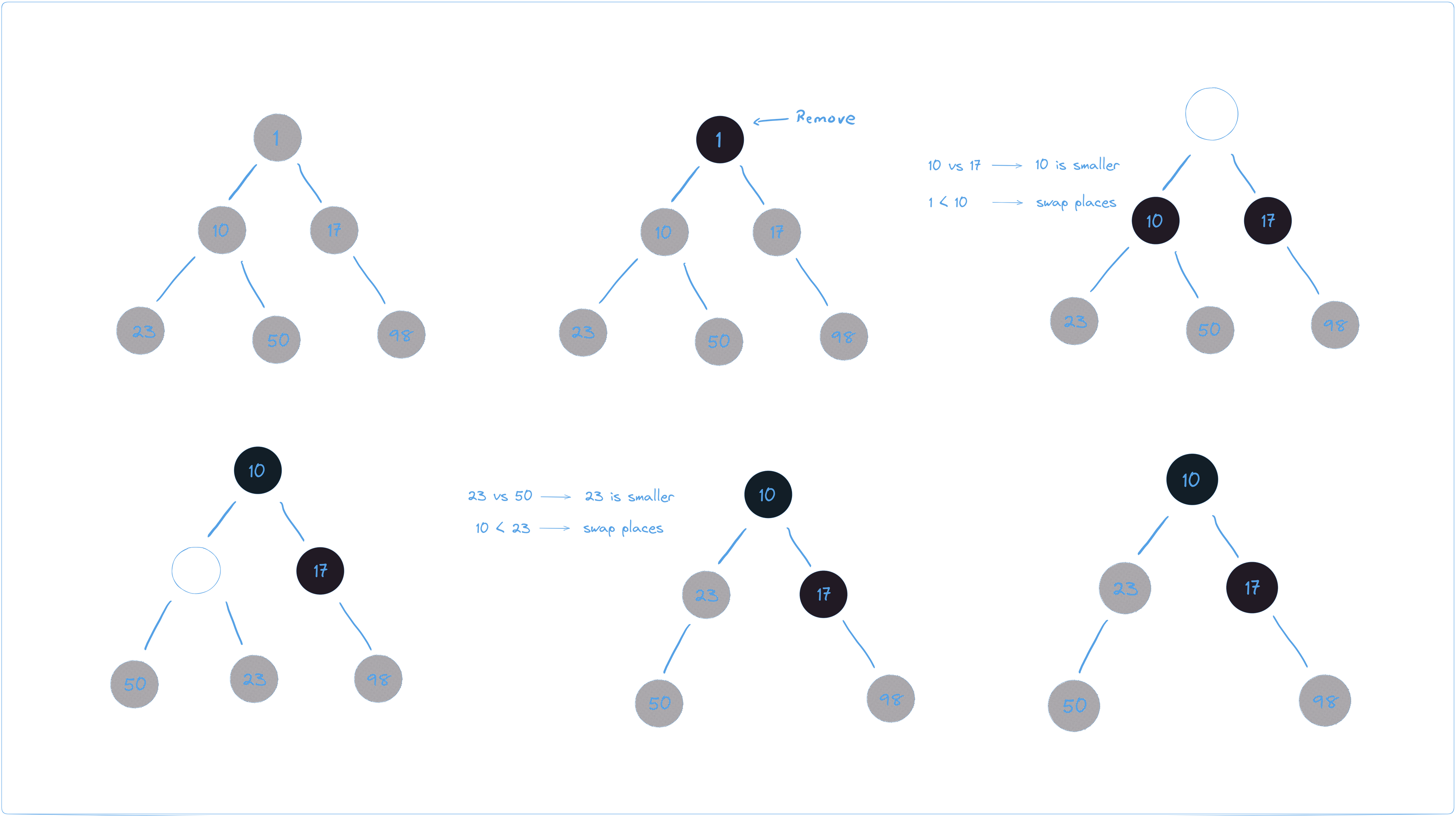
The remove() method checks if the heap is empty. If it's not, it replaces the root node with the last element in the heap, saves the value of the root node, shortens the heap, and calls heapifyDown() to position the new root node correctly.
delete(): number {
if (this.length === 0) {
return -1;
}
let out = this.data[0];
this.length--;
if (this.length === 0) {
this.data = [];
return out;
}
this.data[0] = this.data[this.length];
this.heapifyDown(0);
return out;
}
private heapifyDown(idx: number): void {
const left = this.leftChild(idx);
const right = this.rightChild(idx);
let smallest = idx;
const lValue = this.data[left];
const rValue = this.data[right];
const idxValue = this.data[idx];
if (lValue && lValue < idxValue) {
smallest = left;
}
if (rValue && rValue < this.data[smallest]) {
smallest = right;
}
if (smallest !== idx) {
this.data[idx] = this.data[smallest];
this.data[smallest] = idxValue;
this.heapifyDown(smallest);
}
}
Time and space complexity of heaps
The time complexity of adding an item to a heap is O(log n), where n is the number of items in the heap. This is because the element is added to the end of the array representation of the heap and then "bubbled up" to its correct position, which takes O(log n) time.
The time complexity of removing an item from a heap is also O(log n). This is because the top element is removed and replaced with the last element in the array representation of the heap, and then the new top element is "bubbled down" to its correct position, which also takes O(log n) time.
The space complexity of a heap is O(n), where n is the number of items in the heap. This is because the heap is usually implemented as an array, and the array needs to be large enough to hold all the elements in the heap.
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Insert | O(log n) | O(1) |
| Delete | O(log n) | O(1) |
| Peek | O(1) | O(1) |
| Build | O(n) | O(n) |
export class MinHeap {
public length: number;
private data: number[];
constructor() {
this.data = [];
this.length = 0;
}
insert(value: number): void {
this.data[this.length] = value;
this.heapifyUp(this.length++);
}
print(): number[] {
console.log(this.data.slice(0, this.length));
return this.data.slice(0, this.length);
}
delete(): number {
if (this.length === 0) {
return -1;
}
let out = this.data[0];
this.length--;
if (this.length === 0) {
this.data = [];
return out;
}
this.data[0] = this.data[this.length];
this.heapifyDown(0);
return out;
}
private heapifyDown(idx: number): void {
let lIdx = this.leftChild(idx);
let rIdx = this.rightChild(idx);
if (idx >= this.length || lIdx >= this.length || rIdx >= this.length) {
return;
}
let lValue = this.data[lIdx];
let rValue = this.data[rIdx];
let v = this.data[idx];
if (lValue < rValue && v > lValue) {
this.data[idx] = lValue;
this.data[lIdx] = v;
this.heapifyDown(lIdx);
} else if (rValue < lValue && v > rValue) {
this.data[idx] = rValue;
this.data[rIdx] = v;
this.heapifyDown(rIdx);
}
}
private heapifyUp(idx: number): void {
if (idx === 0) {
return;
}
const p = this.parent(idx);
let pValue = this.data[p];
const v = this.data[idx];
if (pValue > v) {
this.data[idx] = pValue;
this.data[p] = v;
this.heapifyUp(p);
}
}
private leftChild(index: number): number {
return index * 2 + 1;
}
private rightChild(index: number): number {
return index * 2 + 2;
}
private parent(index: number): number {
return Math.floor((index - 1) / 2);
}
}Subscribe to my NewsLetter!
Join my web development newsletter to receive the latest updates, tips, and trends directly in your inbox.
Related Articles
Creating and traversing tries
Tries, also known as prefix trees, are tree-like data structures used for quick string searching.
Exploring Tree Traversals: Depth-First Search and Breadth-First Search Algorithms
Take a deep dive into the world of tree traversal with this article, which covers both depth-first and breadth-first search algorithms.
Exploring more on tree data structures
A helpful guide for anyone interested in learning more about tree data structures, their behavior, and their applications in various fields.
On this page