Iterative Sorting algorithms in Javascript
May 6, 2023Arkar
CS
Lets talk about iterative sorting algorithms in computer science and how to use them.
On this page
Sorting algorithms are important in computer science because they help us organize data so it's easier to work with. I'll discuss three sorting algorithms:
- Insertion sort: a simple sorting algorithm used for small datasets or as part of more complex algorithms.
- Bubble sort: another simple algorithm that's easy to understand and implement, but not as efficient as other sorting algorithms.
- Selection sort: a sorting algorithm that selects the smallest element from an unsorted list in each iteration and places it at the beginning of the list.
I will explain each algorithm in detail, with examples of how they work and their strengths and weaknesses. I'll also provide step-by-step instructions on how to implement each algorithm in your own code. By the end of this post, you'll have a good understanding of interactive sorting algorithms and how they can solve real-world problems.
Insertion Sort
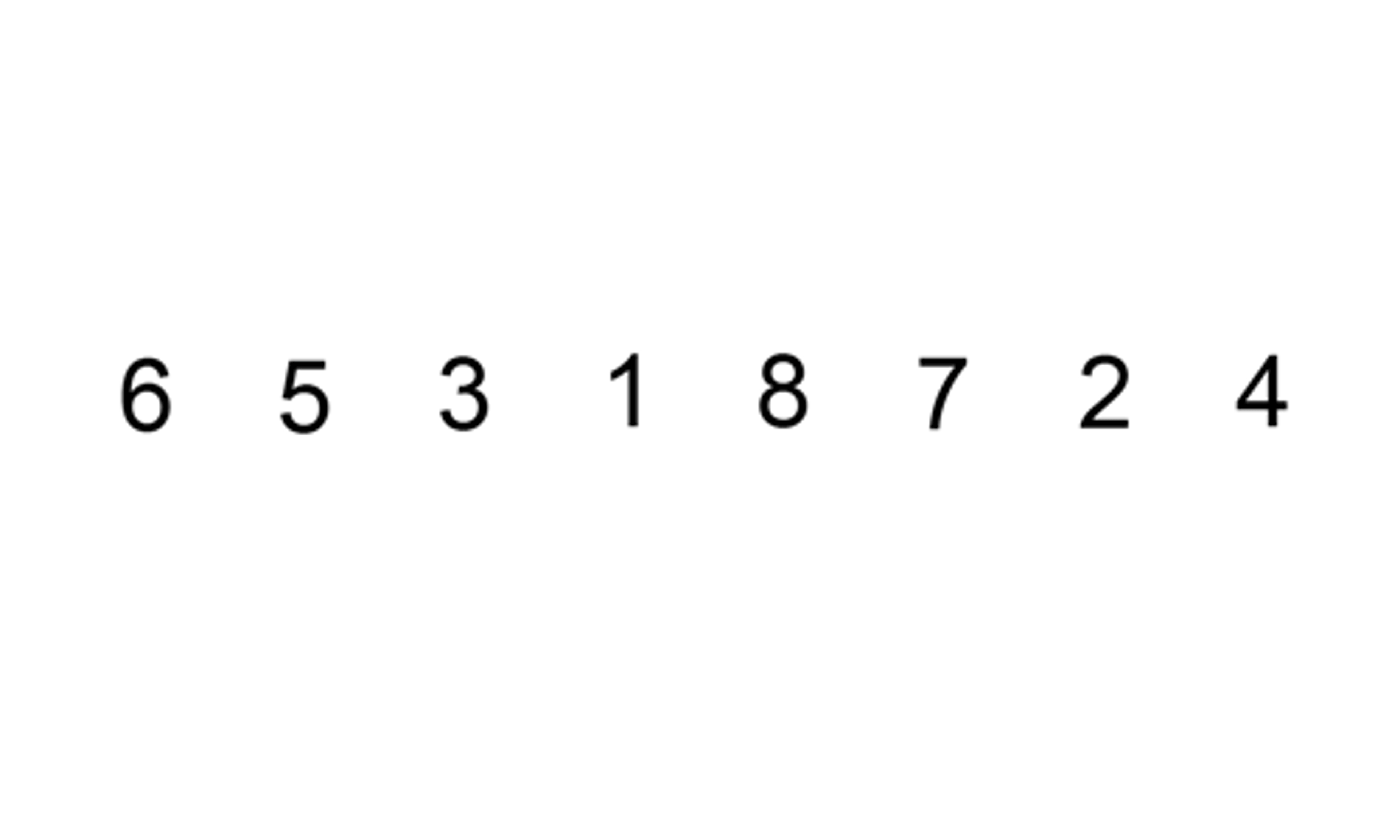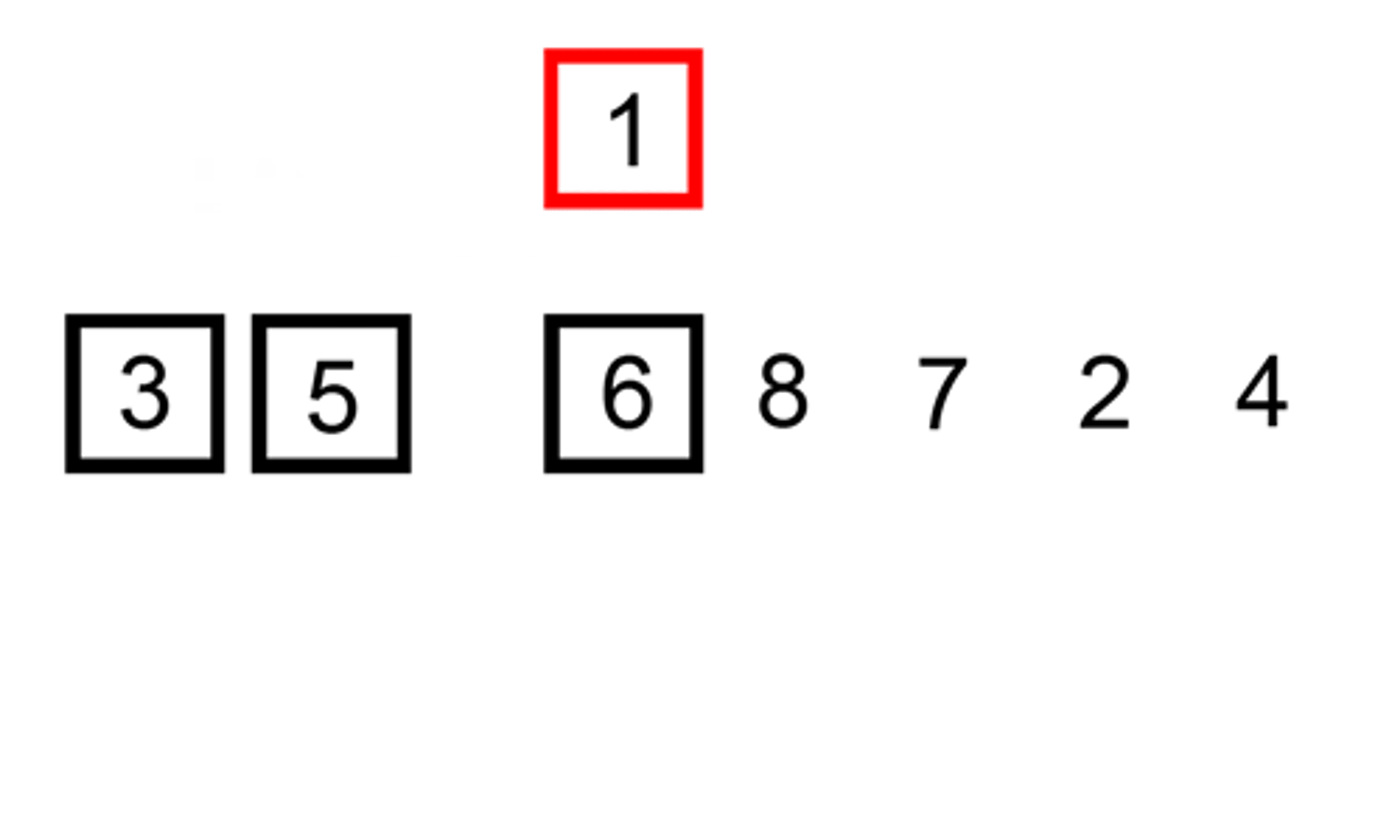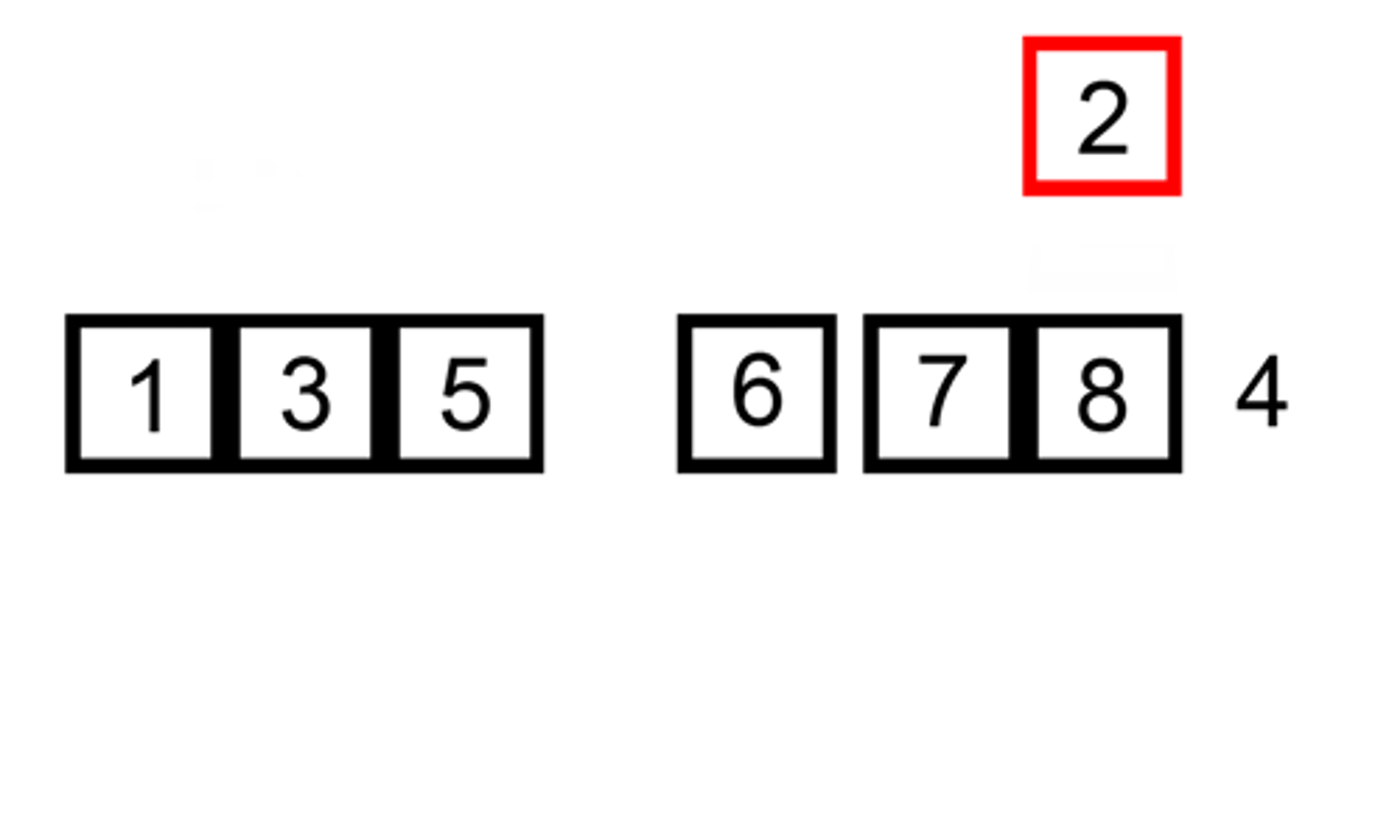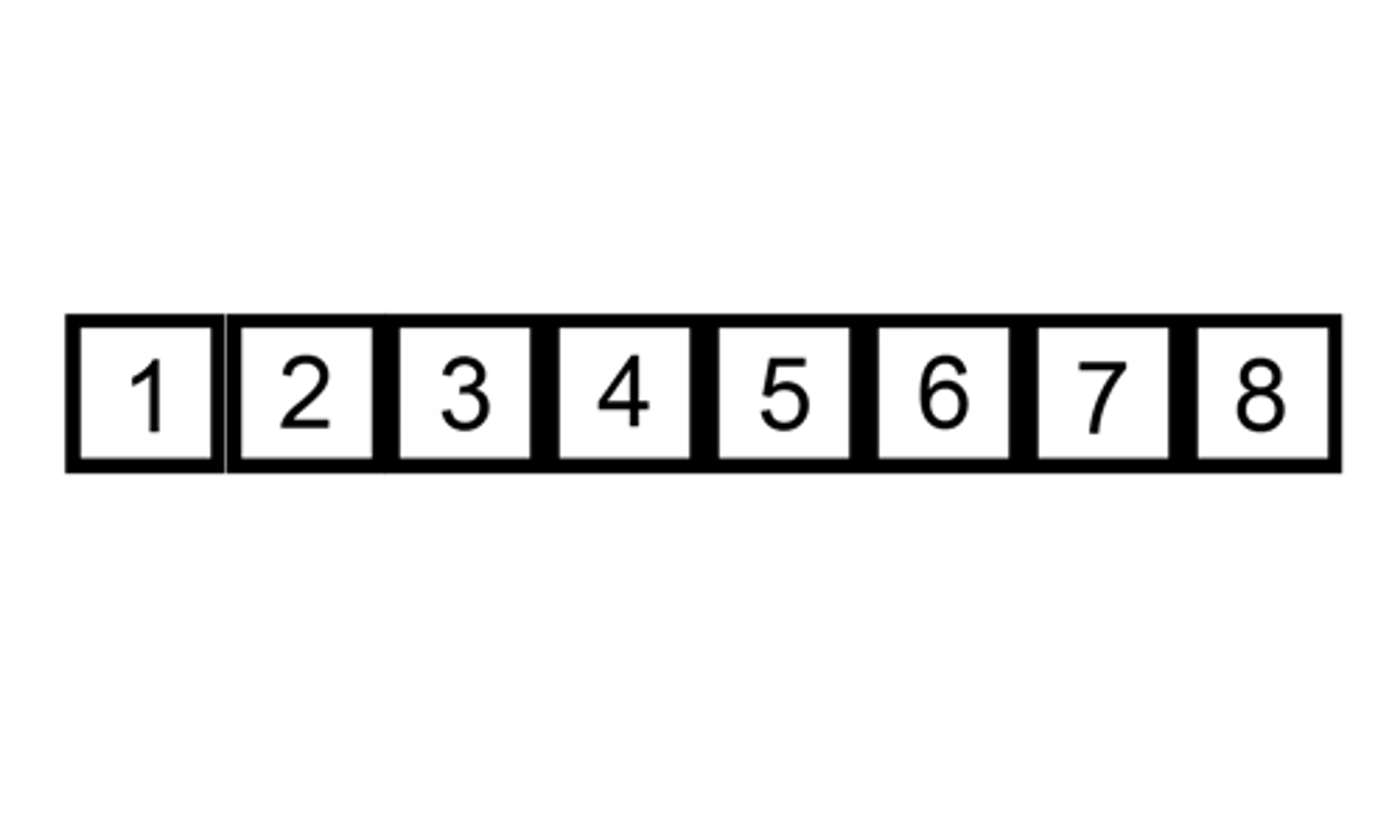
When using insertion sort, it is important to treat the first part of the list as already sorted, and the second part as unsorted.
The algorithm will then begin by considering the first element at index 0 as sorted, and the remaining elements as unsorted. By maintaining this approach, the algorithm can efficiently sort the entire list.
Okay, here's what we do: we'll take the next item - that's the second item at index 1 - and move on to the sorted list. We'll ask, "Is the item I'm about to add larger than the current item?”
If the condition is not met, we move toward the beginning of the list. once we reach the first item, we place the new item at the beginning. We repeat this process for the whole list!
Suppose you have an array [5, 2, 4, 6, 1, 3] that you want to sort in ascending order using insertion sort. The first step is to consider the element at index 0 as the first sorted element, and the remaining elements as unsorted. This means that the first sorted array is [5], and the unsorted array is [2, 4, 6, 1, 3].
5 | 2, 4, 6, 1, 3Next, we’ll take the first element of the unsorted array, which is 2, and compare it to the sorted array [5]. Since 2 is smaller than 5, we insert it before 5, resulting in the sorted array [2, 5] and the unsorted array [4, 6, 1, 3].
2, 5 | 4, 6, 1, 3We then take the next element of the unsorted array, which is 4, and compare it to the sorted array [2, 5]. Since 4 is greater than 2 and less than 5, we insert it between 2 and 5, resulting in the sorted array [2, 4, 5] and the unsorted array [6, 1, 3].
2, 4, 5 | 6, 1, 3We repeat this process for all the remaining elements of the unsorted array. The next element is 6, which is greater than all the sorted elements, so we insert it at the end of the sorted array, resulting in the sorted array [2, 4, 5, 6] and the unsorted array [1, 3].
2, 4, 5, 6 | 1, 3The next element is 1, which is smaller than all the sorted elements, so we insert it at the beginning of the sorted array, resulting in the sorted array [1, 2, 4, 5, 6] and the unsorted array [3].
1, 2, 4, 5, 6 | 3Finally, we insert the last element, 3, between 2 and 4, resulting in the sorted array [1, 2, 3, 4, 5, 6].
Time and Space complexity of insertion sort
Let’s talk about the best and worst cases of insertion sort. In the worst-case scenario, where the list is in reverse sorted order, insertion sort will have to compare each element to every other element in the sorted portion of the list before inserting it in its correct place. This means that in the worst-case scenario, insertion sort has a time complexity of .
In the best case, the list is already sorted, and the algorithm can simply go through the list without having to move any elements. In this case, the time complexity of the insertion sort is . However, it's important to note that the best case is rare and often not the case in real-world scenarios. Also, the worst case is much more important to consider when analyzing the efficiency of an algorithm.
| Algorithm | Best Case Time | Average Case Time | Worst Case Time | Space Complexity |
|---|---|---|---|---|
| Insertion Sort | O(n) | O(n^2) | O(n^2) | O(1) |
When should you use insertion sort? Insertion sort is best for small data sets or data sets that are almost sorted. For larger data sets, insertion sort can become quite slow.
Note that the space complexity of the insertion sort is because the algorithm does not create any additional space beyond the input array. This can be an advantage over other algorithms that require additional space for sorting.
In general, if you are dealing with large data sets, you may want to consider using a more efficient sorting algorithm, such as quicksort or mergesort which I will be discussing later in the blog.
However, if you're working with a smaller data set or a data set that is already partially sorted, insertion sort can be a good choice. Additionally, because of its simplicity, insertion sort can be a good choice for educational purposes or for situations where code readability is more important than efficiency.
export function insertion_sort(arr: number[]) {
let length = arr.length;
for (let i = 0; i < length; i++) {
let j = i - 1;
let current = arr[i];
while (j > -1 && arr[j] > current) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = current;
}
return arr;
}Bubble Sort
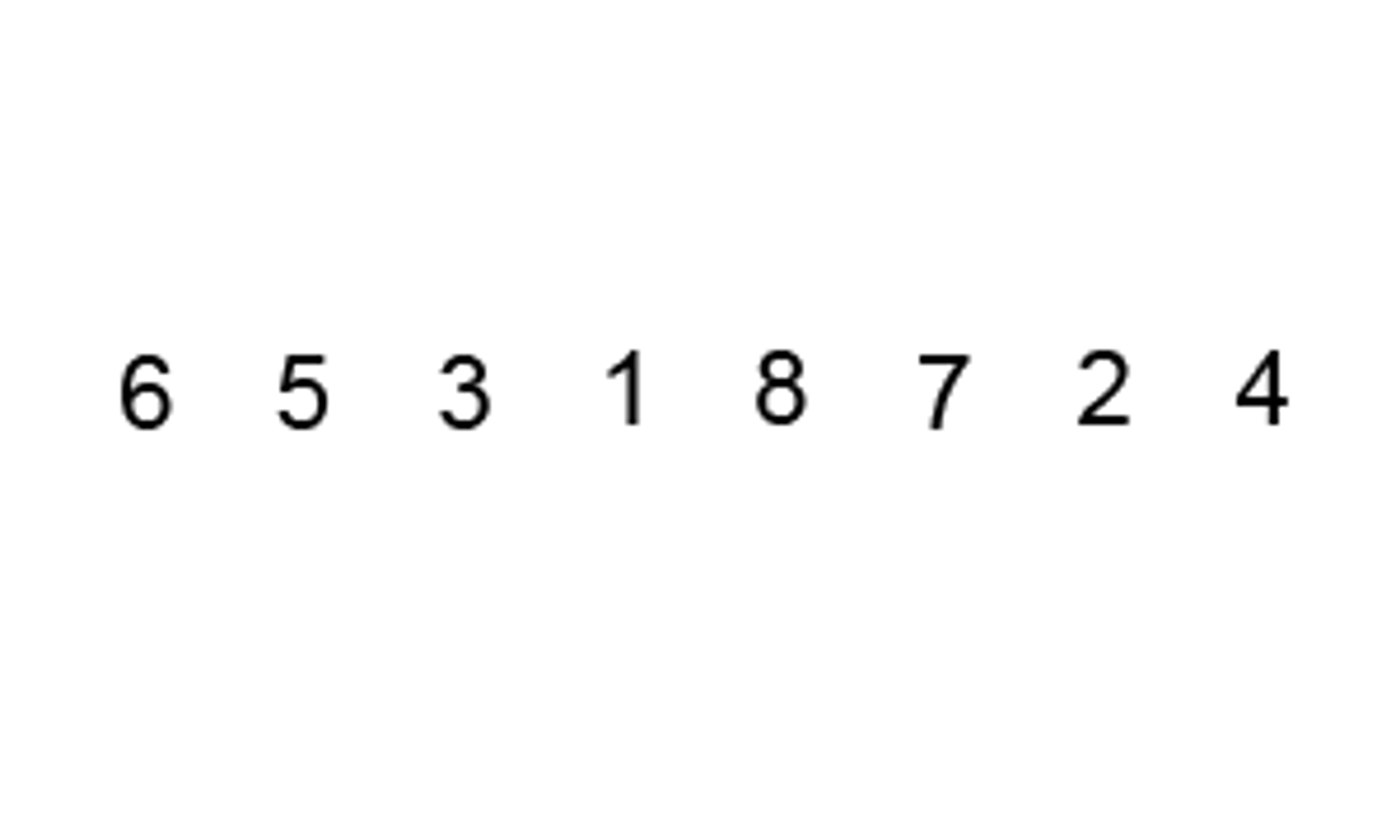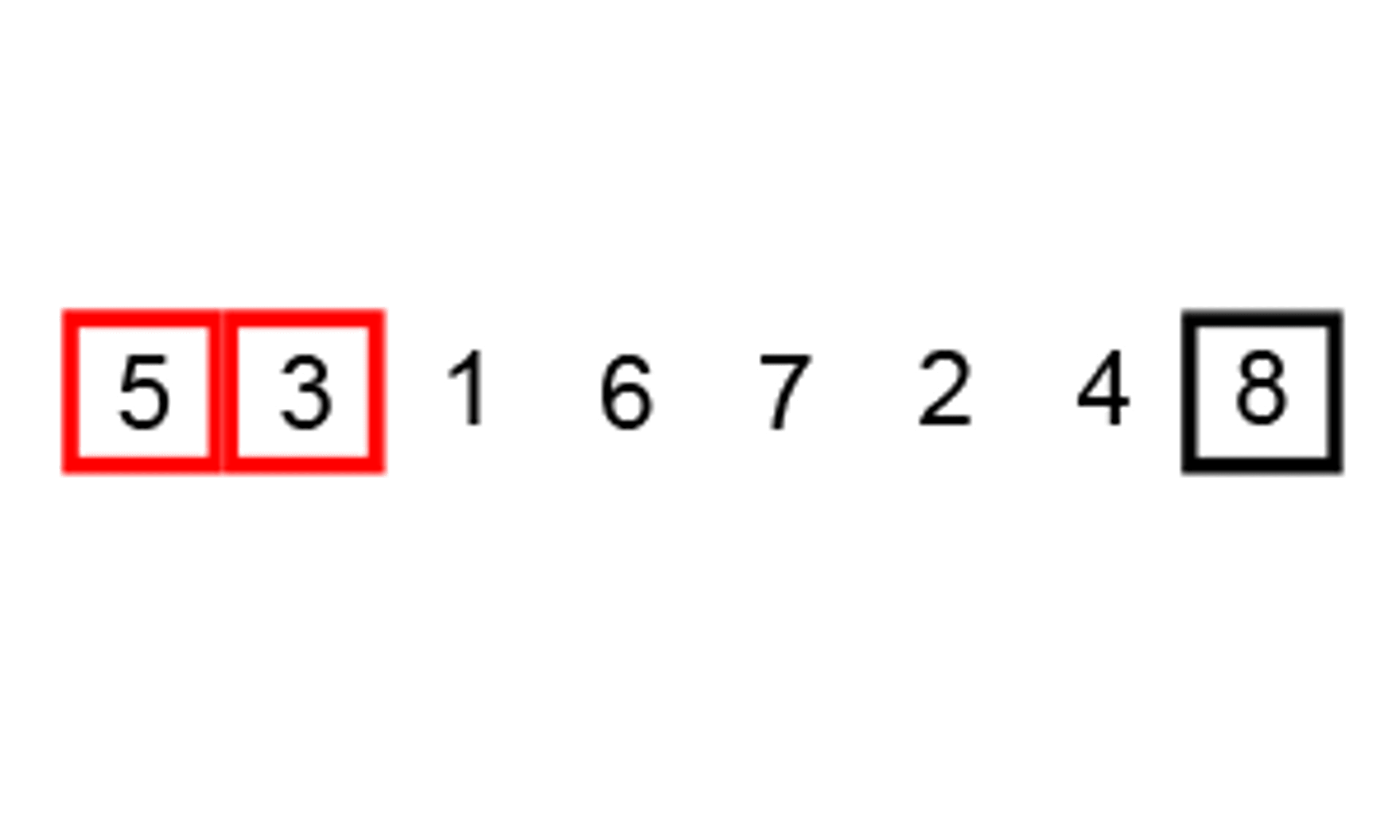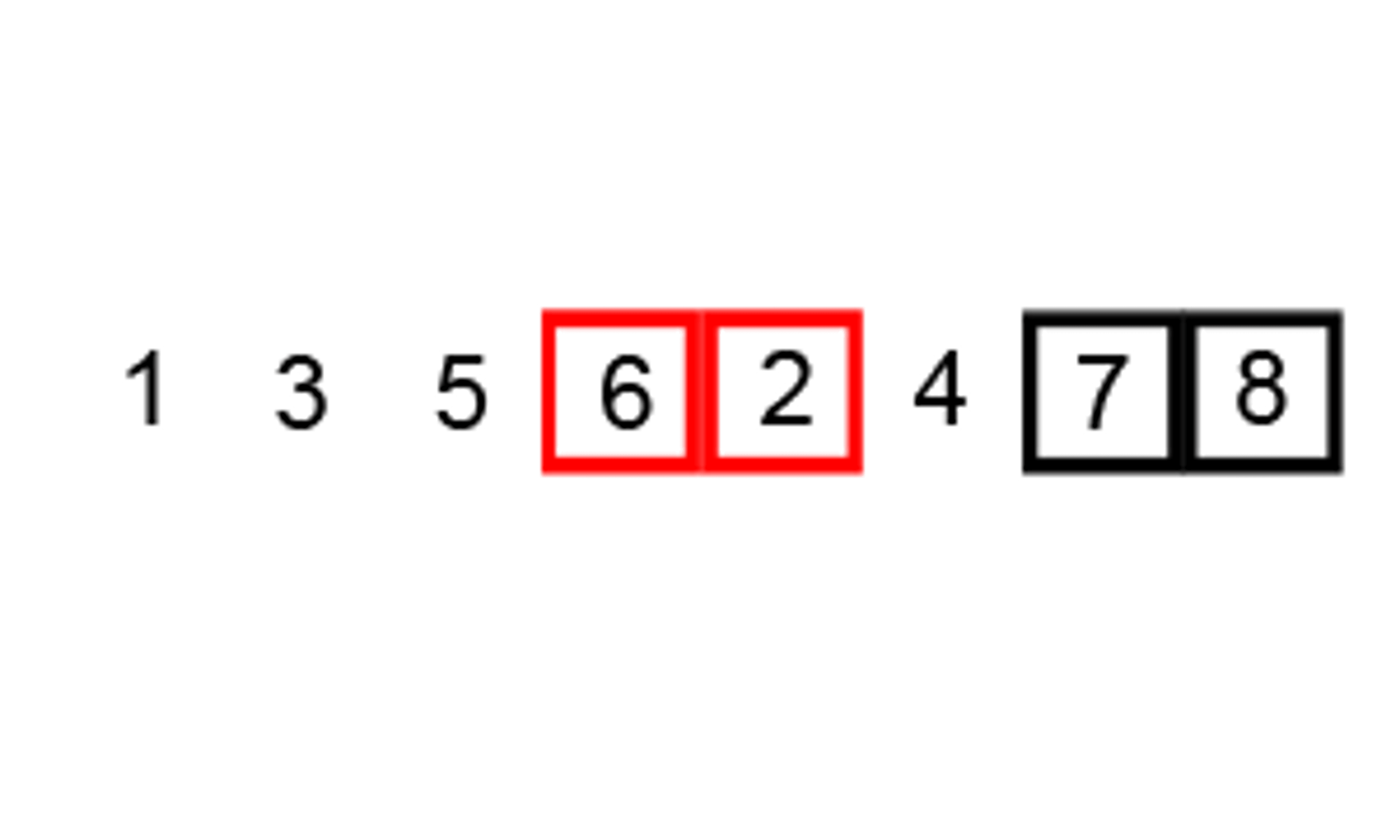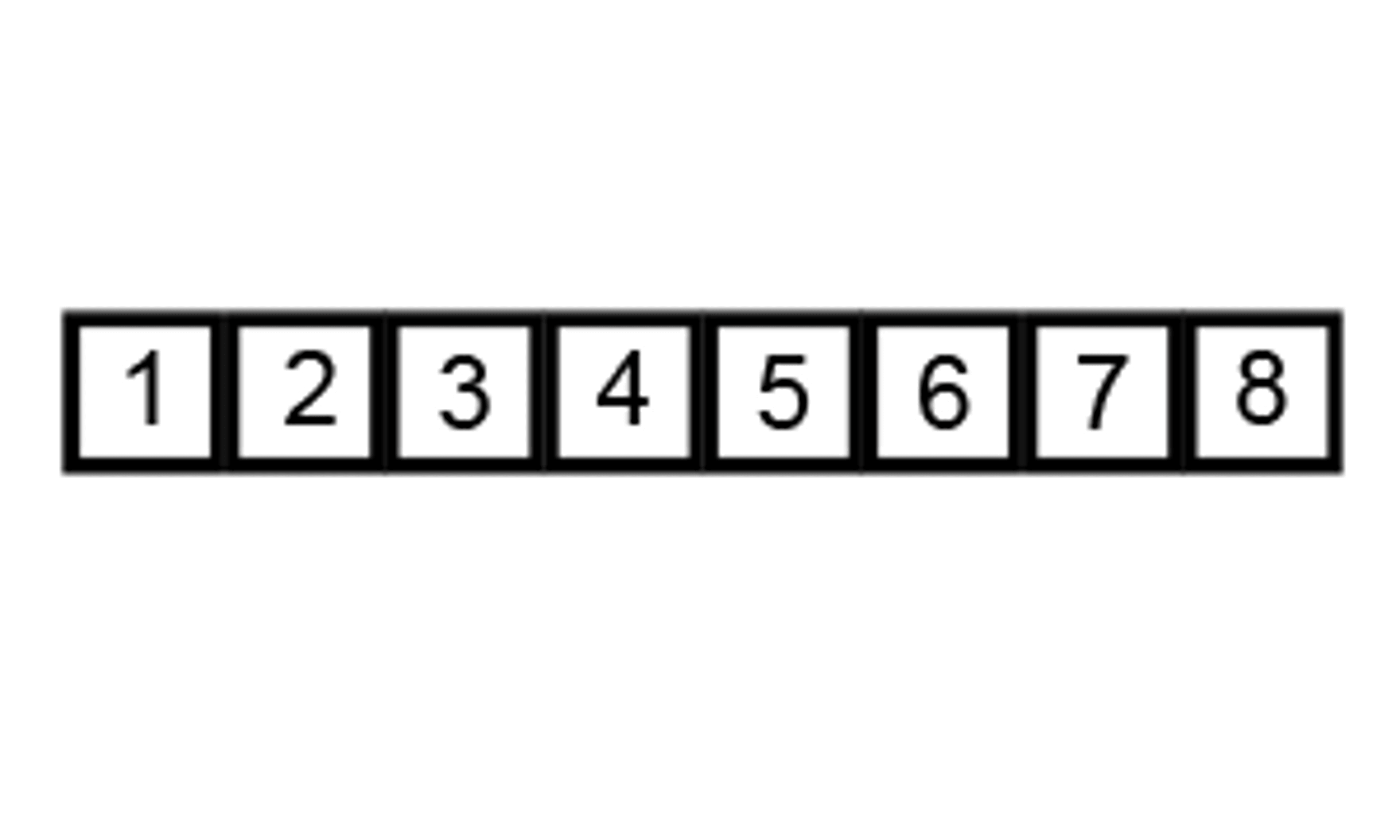
Bubble sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent pairs, and swaps them if they are in the wrong order. This sorting algorithm is named bubble sort because smaller elements bubble to the top of the list.
The algorithm works by repeatedly swapping adjacent elements if they are in the wrong order. The algorithm starts at the beginning of the list and compares the first two elements. If the first element is greater than the second element, the algorithm swaps them. The algorithm then moves on to the next pair of elements and repeats the process until the end of the list is reached.
At this point, the algorithm starts again from the beginning of the list and repeats the process until no more swaps are needed. This indicates that the list is sorted.
Bubble sort has a time complexity of in both the best and worst cases, and a space complexity of . Like insertion sort. bubble sort is also best suited for small data sets or data sets that are almost sorted.
Suppose we have an array [5, 3, 1, 8, 7] that we want to sort in ascending order using bubble sort. The first step is to compare the first two elements of the array, which are 5 and 3. Since 5 is greater than 3, we need to swap these elements.
[5, 3] -> [3, 5]We then compare the next two elements of the array, which are 5 and 1. Since 5 is greater than 1, we need to swap these elements.
[3, 5, 1] -> [3, 1, 5]We continue this process until we have compared all adjacent pairs of elements in the array. At this point, the largest element in the array, which is 8, will have "bubbled" to the end of the array.
[3, 1, 5, 8, 7]We then repeat the process, starting from the beginning of the array. We compare the first two elements of the array, which are 3 and 1. Since 3 is greater than 1, we need to swap these elements.
[3, 1, 5, 8, 7] -> [1, 3, 5, 8, 7]We then compare the next two elements of the array, which are 3 and 5. These elements are in the correct order, so we do not need to swap them.
[1, 3, 5, 8, 7]We continue this process until we have compared all adjacent pairs of elements in the array and no swaps are needed. This indicates that the array is sorted.
Time and space complexity of bubble sort
| Algorithm | Best Case Time | Average Case Time | Worst Case Time | Space Complexity |
|---|---|---|---|---|
| Bubble Sort | O(n) | O(n^2) | O(n^2) | O(1) |
In the basic implementation of bubble sort, the algorithm iterates through the entire list, even if it is already sorted. As a result, it makes unnecessary comparisons and swaps. Bubble sort will run even if the array is already sorted. We can add small optimizations for such cases as well.
In bubble sort, we make sure that after each iteration, the biggest number is in its correct place. This means that the last part of the array is already sorted. Therefore, we don't need to check if 8 and 9 are out of order during the second run-through of the array. We can check one less element each iteration because we know that we already have one guaranteed element in its correct place at the end of each iteration.
You can also add a flag that keeps track of whether any swaps were made during a particular iteration. Bubble sort will run even if the array is already sorted If no swaps were made, this means that the list is already sorted, and the algorithm can terminate early. This optimization can significantly reduce the number of iterations required, especially for larger data sets that are partially sorted.
export function bubble_sort(arr: number[]) {
let swapped = false;
for (let i = 0; i < arr.length; i++) {
for (let j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
let tmp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = tmp;
swapped = true;
}
}
if (!swapped) {
return arr;
}
}
return arr;
}Selection Sort
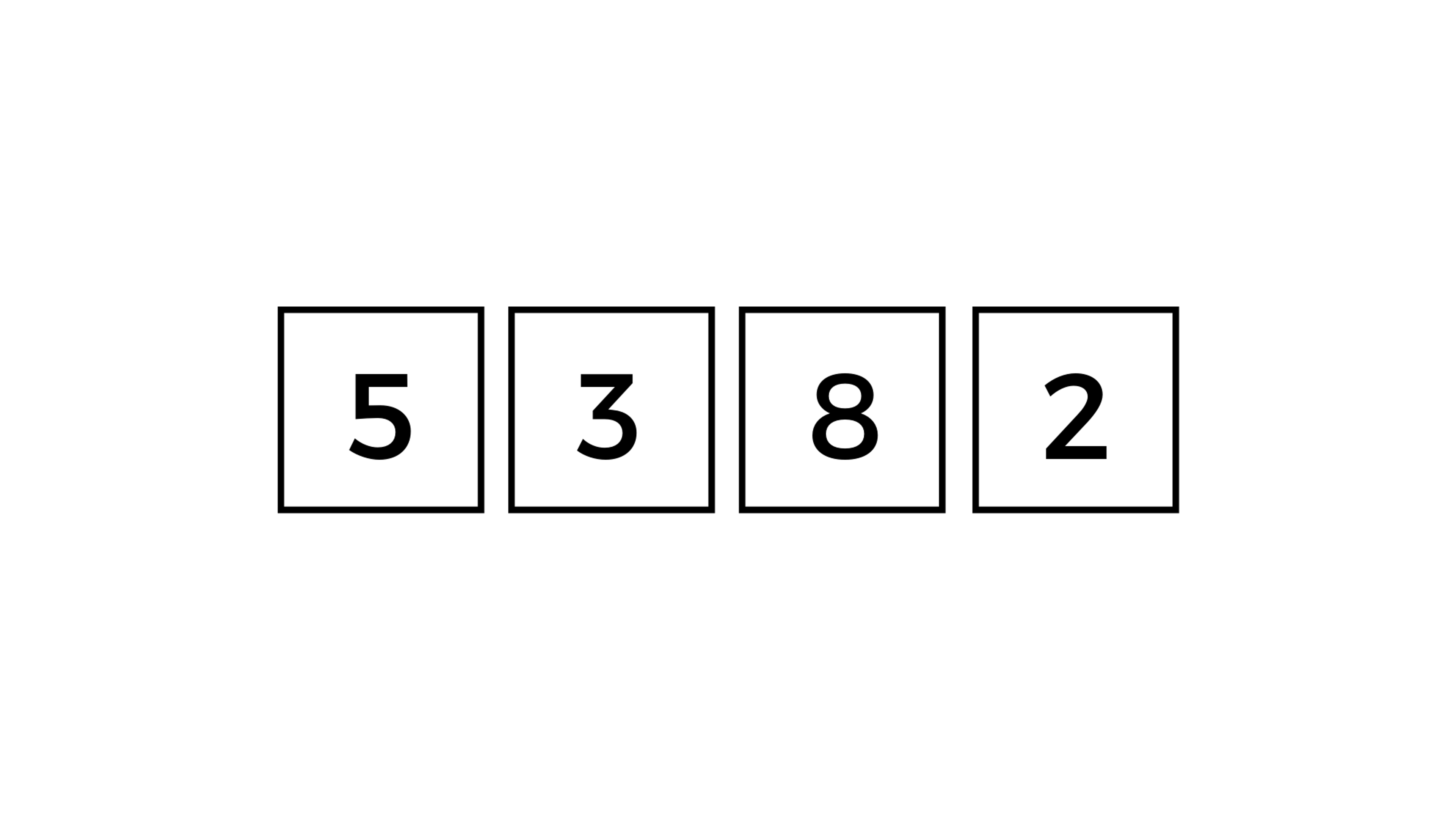
Selection sort is a basic way to sort a list. It works by finding the smallest number in the unsorted part of the list, then moving that number to the beginning of the list. The algorithm keeps repeating this process for the rest of the unsorted part of the list until the entire list is sorted.
Suppose we have an array [64, 25, 12, 22, 11] that we want to sort in ascending order using selection sort. The first step is to find the smallest element in the array, which is 11. We then swap it with the first element of the array, which gives us the sorted array [11, 25, 12, 22, 64] and the unsorted array [25, 12, 22, 64].
11 | 25, 12, 22, 64Next, we need to find the smallest element in the unsorted array, which is 12. We swap it with the second element of the array, resulting in the sorted array [11, 12, 25, 22, 64] and the unsorted array [25, 22, 64].
11, 12 | 25, 22, 64We repeat this process for all the remaining elements of the unsorted array. The next smallest element is 22, which we swap with the third element of the array, resulting in the sorted array [11, 12, 22, 25, 64] and the unsorted array [25, 64]
11, 12, 22 | 25, 64We repeat this process until the entire array is sorted. The next smallest element is 25, which we swap with the fourth element of the array, resulting in the sorted array [11, 12, 22, 25, 64] and the unsorted array [64].
11, 12, 22, 25 | 64Finally, we swap the last two elements of the array, resulting in the sorted array [11, 12, 22, 25, 64].
Time and Space complexity of selection sort
| Algorithm | Best Case Time | Average Case Time | Worst Case Time | Space Complexity |
|---|---|---|---|---|
| Selection Sort | O(n^2) | O(n^2) | O(n^2) | O(1) |
Selection sort is not the best sorting algorithm for larger data sets as it has a time complexity of in all cases, even if the list is already sorted. However, it can still be useful for small data sets or in cases where memory usage is a concern because it has a space complexity of - it doesn't require any additional space beyond the input array.
function selection_sort(arr: number[]) {
let length = arr.length;
for (let i = 0; i < length - 1; i++) {
let min = i;
for (let j = i + 1; j < length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min != i) {
[arr[i], arr[min]] = [arr[min], arr[i]];
}
}
return arr;
}Iterative sorting algorithms are essential in computer science and it's important for programmers to understand them. I just think they are fun to learn !
Have fun sorting! ✨
Subscribe to my newsletter
Join my web development newsletter to receive the latest updates, tips, and trends directly in your inbox.
On this page